Analysis of Derivative Contracts in Trading Business

To fully understand this analysis, you will need to read Analysis of Exchange Trading, Sections 1 and 2 first.

Derivative financial trades are gaming an increasingly prominent role in trading. A derivative trade is one whose value depends on another security's value. The simpler forms of derivatives have been around for quite a while; for example, stock options were first traded on an organized exchange in 1973.
Since then, more and more exotic variants of derivatives have appeared. They are valuable to investors because they reduce the risk that comes from changing prices. However, when they are not properly controlled, derivatives can be dangerous: Recently, in several famous cases, organizations have lost spectacular amounts of money on ill-managed derivatives.

Modeling derivatives brings out many useful aspects of modeling because derivatives form a natural generalization hierarchy - one that is more interesting than the usual examples of plants and animals. The purpose of this analysis, therefore, is to explore some of the problems of this kind of generalization hierarchy using derivatives as examples.

We begin by introducing the simple derivatives: Forward Contracts (Section 1) and Options (Section 2).
Forward contracts introduce the notion of tenor, which leads to a discussion of why date calculations are more complicated than adding up days.
Options present a couple of awkward modeling areas: handling the trader's definitions of calls and puts, and the relationship between an option and the underlying contract.

A more complex type of derivative, the combination option, can be seen as an aggregation of simpler options. Sub-typing from options with the composite pattern is not always effective; this leads to the Product (Section 3) pattern. This pattern is based on the difference between the seller's and trader's views of the deal and can be applied to regular trading as well. It also serves as an example of how generalization is often the first method we think of using but is not necessarily the best.

With sub-typing we must ensure that the sub-type's behavior is consistent with that of the super-type. Using barrier options as an example, we will explore how sub-typing and state charts interact with Sub-type State Machines (Section 4).

If we have a portfolio of options, we can choose to have a browser that highlights pertinent details, depending on the kind of option. This leads to a situation where there are parallel application and Domain Hierarchies (Section 5). The two hierarchies are awkwardly coupled.
This pattern poses a problem with several solutions, none of which is all-powerful.

Key Concepts: Forward Contract, Tenor, Option, Product

1. Forward Contracts

The contracts discussed in Analysis of Exchange Trading, Section 1 are simple and involved in immediate deals. Most markets involve a range of more complex deals.
The simplest of these is the forward contract. With a normal contract, often referred to as a spot contract, delivery occurs as close as possible to the date on which the contract is traded. Delivery usually occurs in a couple of days. Forward contracts are agreements to do a deal some time in the future.
For example, a company is due to receive a tanker full of oil in two months. The company will have to pay several million dollars for this oil.
However, if the company is German, its normal financing is done in marks. If the dollar/mark exchange rate changes significantly in the next two months, the company could find itself having to pay more marks than it expected, which could be a significant problem. Of course, the company would also gain from a favorable change in exchange rates; but the uncertainty is not good for the company. To allay this uncertainty, the company could choose to buy several million dollars in a forward contract exchange rate deal, paying an agreed amount of marks now for delivery of dollars in two months.
The price is offered by the bank who is carrying out the deal based on the market's perception of where the dollar/ mark rate is likely to go in the next couple of months. Such a deal is said to have a tenor of two months (as opposed to a tenor of spot).

A forward contract is quite easily captured by holding separate trade and delivery dates for the contract, as shown in Figure 1. A spot deal will have suitably close trade and delivery dates, while a forward contract deal will have these dates separated by two months. A sub-type is not needed to show this, although we can add one for clarity.


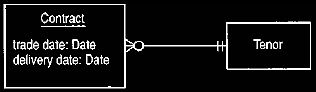
Figure 1. A contract that can support forward contracts.
The tenor is based on the difference between trade and delivery dates.

Example: Aroma Coffee Makers agrees on January 1, 2007 to buy 5000 tons of Bra zilian coffee from Brazil Coffee Exports.
Delivery is set for October 20, 2007, and the price is set at today's price.

Example: we buy an airline ticket for travel in three months, paying the price currently quoted for the journey.

An important consideration when discussing forward contracts is the tenor of the contract. The tenor is the period between the trade date and the delivery date, in our example two months. Prices are generally quoted on the market with a particular tenor in mind, and the tenor is an important part of the contract's consideration. However, the tenor is not simply the duration between trade and delivery dates. If our two-month contract is traded on May 4, the delivery date will not be on July 4, simply because the 4th of July is a holiday in the United States. Holidays have a big impact on how these dates are calculated.
Assuming July 4 does not fall on a weekend, a two-month contract dealt on May 4 will take delivery on July 5. Note that if for some reason Germany had a holiday on July 5, the delivery date would be shifted forward another day. The contract still has a tenor of two months, even though its delivery date is the same as a contract with a delivery date of two months and one day. Note that this behavior is required for spot contracts as well: a deal done on a Thursday will be delivered on a Monday (unless it is a holiday) even though spot is taken as two days. Hence Figure 1 includes trade date, delivery date, and tenor.

In this kind of structure, the calculation of the delivery date is not something that can be done by the trade date and tenor alone. Without considering holidays, we can determine the delivery date by a simple calculation between date and tenor. However, the market holidays have to be taken into account. This means that the market has a date calculation routine that allows it to adjust for holidays, as shown in Figure 2. This consideration of holidays is an important feature in many areas, where the concept of working days becomes important. It is usually not possible to determine working days globally because holidays vary from country to country, or possibly with even greater granularity. Individual sites may also have local holiday conventions that will affect working day calculations.


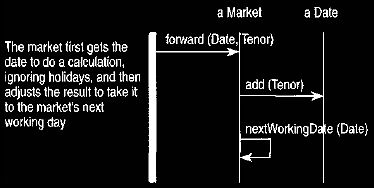
Figure 2. Getting the market to calculate dates.
Date calculations often need to be delegated to another object when working days need to be calculated.

Example: A company needs to make a payment to an employee within five working days from June 30,2007.
If it is a US company, this is by July 8 (skipping over weekends and July 4); for a UK company it is July 7.

Modeling Principle: Date calculations are often affected by holidays, which need to be skipped over.
Holidays vary from country to country and often by the organizations involved.

2. Options

For our German oil company, a forward contract is a valuable tool for reducing the risk of an exchange rate change that would cause them to pay more for their oil. But the company does run the risk of losing out should the exchange rate change in their favor. Financial directors essentially have to bet on the exchange rate movement. If they think the mark will go up, they should buy on the spot market; if they think it will go down, they should buy forward contracts.
Options reduce this risk. An option gives the buyer the right to buy dollars at a prearranged exchange rate if the holder wishes. Thus, if the mark goes down, the oil company can exercise its option and buy the dollars at the prearranged price; if the dollar goes up they can ignore their option (let it expire) and buy on the spot market. The bank charges a premium to the oil company to sell them the option, so the bank now manages the risk. Since the bank handles many such deals, they can offset the risks of various deals against each other. Figures 3 and 4 describe the behavior of an option.


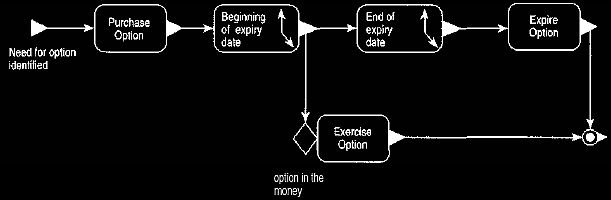
Figure 3. Event diagram for the process of using an option.
An option can only be exercised after the start of the expiration date and will only be exercised if it is "in the money," that is,
if exercising the option is a better deal than a spot trade at the current price.


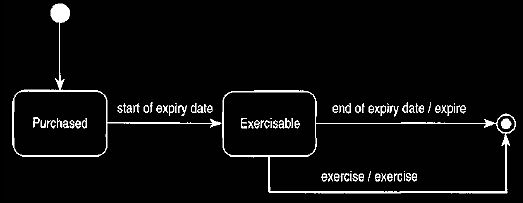
Figure 4. Harel state chart to illustrate how an option behaves.
The option can only be exercised on its expiration date (a "European" option).

Many features of the option are similar to that of a normal contract. Like a normal contract, options have counterparties and trade dates. Other features of the option include the expiration date, the amount of premium, and date the premium is delivered.

Thus we can consider an option to be a sub-type of a contract, as shown in Figure 5. A key feature of the option structure is the polymorphic operation value (Scenario). The value of a spot contract is easy to understand because it is simply the result of applying the spot exchange rate in the provided scenario to the amount of the contract. Options are rather more complex to value, to put it mildly. The most common technique is Black-Scholes analysis. An explanation of this is beyond the scope of this book, except to point out that as far as the caller of this operation is concerned, it is a single operation.
The complexities of the mathematics can safely be hidden within the operation.


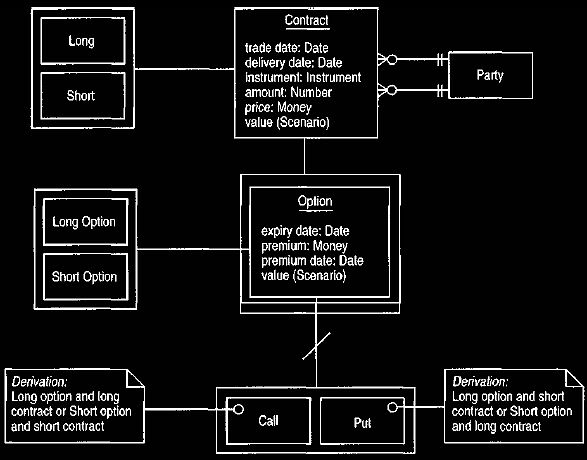
Figure 5. Structure of an option.
Call and put are terms derived from the longs and shorts.

2.1 Longs, Shorts, Calls, and Puts: Representing a Tricky Vocabulary
The question of longs and shorts does need discussion. In Analysis of Exchange Trading, Section 1 we explained that a contract can be long (buy) or short (sell).
For options, however, we find that there are four possible choices. We can sell an option to sell money, sell an option to buy money, buy an option to sell money, or buy an option to buy money. The long/short choice still exists on the contract, but it is supplemented by a further long/short choice on the option. The trader's vocabulary includes the terms call and put. A call is an option to buy (that is, a long contract), while a put is an option to sell (a short contract).
Naturally we can buy or sell a call, or buy or sell a put. Representing this language is somewhat tricky, as well as confusing.

If we sell an option to buy yen, then the counterparty can buy yen from us at the expiration date. The difference between this and a forward is that the counterparty can choose not to. If we buy an option to sell yen, then the position is the same, but the control over exercising the option is now mine. Either way, we are (potentially) short on yen, hence the contract is short. In the former the option is also short, while in the latter the option is long. In the first case traders would say they are selling (short) a call, and in the second they would say they are buying (long) a put.

One way of looking at this would be to say that we could replace the long/ short description of a contract by call/put. But this does not really work because we do not use the terms call and put on contracts that are not options.

Another possibility is to use the terms long and short for options only to indicate the state of the option rather than the contract. Thus the first example above would be a short call and the second a long put. This might make sense to a trader but would be apt to confuse any software. When evaluating risk, the position of the amount of the contract is important, and in the above examples both are short. Hence we need to be able to ask the direction of the contract (which defines the position), the direction of the option, and the call/put. So the two examples are (short contract, short option, call) and (short contract, long option, put). Clearly one of these can be derived from the other two. The diagram indicates that call/put is derived. The derivation is a reminder that one is derived rather than any direction to an implementor of what is actually stored or calculated in the implementation.

Representing language like this is always a bit of a battle, particularly when it seems unnecessarily illogical. The important thing is to represent the fundamentals in a logical manner. These fundamentals may be part of the domain expert's terminology or invented during the modeling process (but if they are invented, the domain expert must be comfortable with them). The rest of the terminology can then be derived from these fundamentals.

Modeling Principle: Derived markers should be used to define terminology that is derived from other constructs on the model.

Modeling Principle: Marking a feature as derived is a constraint on the interface. It does not affect the underlying data structures.

Example: On June 1, 2007, we are given an option to buy 200 shares of Aroma Coffee Makers on January 1,2009 at a price of $5 per share.
This is an option with a trade date of June 1, 2007, an instrument of Aroma Coffee Makers stock, an amount of 200, delivery and expiration dates of January 1,2009, a premium of $0, and a price of $5.1 will gain shares, so the contract is long (with respect to us), and the option is also long (since we hold it); it is thus a call.

Example: When we make a reservation for a flight, we are being given a call option on the ticket.
The expiration date of the option is the date the reservation must be ticketed.

Another concern is the interaction between delivery date and expiration date. For an option, the delivery date can be computed if the expiration date is known (delivery date = expiration date + spot). The reverse is not true, however (due to the interference of holidays). This means that, for options, delivery date is a computed mapping. The important point here is that the interface does not change: There is still an accessor for delivery date; however, the information is stored. There are two alternatives to describe this situation: We can note (typically in the glossary) that for options the delivery date attribute is overridden and calculated from the expiration date according to the formula. Another option is to describe the formula as a constraint on the option type. Both are perfectly reasonable and the choice is a matter of taste. It is entirely up to the implementor what code and data structure to use.

2.2 To Sub-type or Not to Sub-type
The structure shown in Figure 5 is not the only way to handle options; another choice is shown in Figure 6. The difference between the two structures is how the optionality is added to the contract. In Figure 5 we add it by sub-typing. In this scheme an option is a kind of contract with additional properties and some variant behavior. In Figure 6 we may say that an option has a base contract often referred to by traders as the underlying of the option.
There is at least some notion of containment here, especially in the fact that we would not be likely to ask the contract to value itself if it was an underlying to an option. Similarly the delivery date would be dependent on the option's expiration date.

The choice between the two structures is not easy. Both have elegant qualities. The Figure 6 model separates the notion of option and contract with a definite notion of underlying. One disadvantage of this scheme is that a single contract is represented by two objects. It is easier to alter Figure 6 to handle compound options (options where the underlying is an option). With so little choice between them, we can easily end up getting bogged down.
Prototyping can sometimes clarify the situation but not always. When alternatives like this present themselves, it's a good idea to use the simpler approach and then change to the more complicated one later if necessary. With this case, however, it is arguable which is the simpler.
When it is this close, we trust the domain experts' instincts by asking them which feels best. We will continue to use Figure 5 as the basis for further discussion.

Modeling Principle: When faced with alternative approaches, choose the simplest first and change to a more complex one as needed.

Modeling Principle: When there is little to choose between modeling alternatives, follow the instincts of the domain expert.



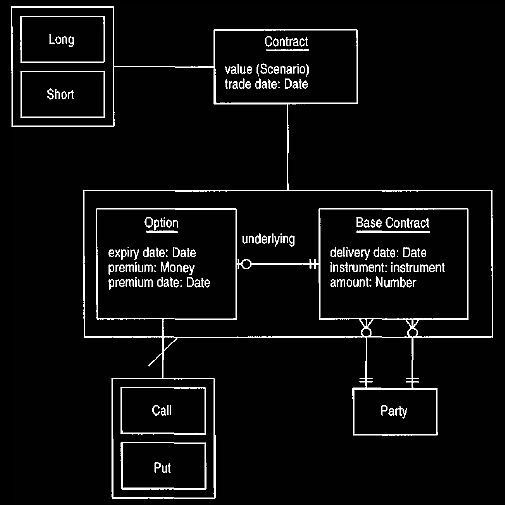
Figure 6. The separate object approach to options and contracts.
Both this and Figure 5 are reasonable alternatives, although this analysis builds on Figure 5.

3. Product

Derivative trades have long been considered somewhat risky, mainly because of the complex mathematics required to evaluate risk. The Black-Scholes equation which serves as the building block for much of the evaluation process, is a second-order partial differential equation. Even with an engineering background, these animals still give us the willies.

The most spectacular example of the pitfalls of derivatives trading is the collapse of Britain's venerable Barings Bank. According to current reports, the primary cause of the collapse was dealing in a particular kind of derivative called a straddle—an example of a combination option. Combination options can be seen as a composite of other options. It seems appropriate to discuss this section with straddles as an example.

The concept of a straddle is in fact very simple. You have a holding worth some $70 million, depending on prices, and you are concerned about any large change in its value over the next three months. Either going up or down will cause a problem. To avoid the problem, you can buy a call and a put, both with a price of $70 million and an expiration in three months. Let's assume the premium on each of these is $2.5 million. If the price goes up you exercise the call and you gain the value of the holding at the new price, less $70 million and the $5 million total premium. Thus if the value of the holding rises above $75 million you are happy. Similarly if the value falls below $65 million you are happy. The worst thing that can happen is that the price stays steady, in which case you lose the $5 million premium. The attractiveness of a straddle comes from a fixed risk that covers an otherwise very wide range of movement.
Naturally a very volatile instrument can result in a higher premium for the straddle, but if you are trying to reduce your risk in a volatile environment, this can be a very useful product.

If you are the seller, of course, you are faced with a more tricky prospect: You can lose an unlimited amount of money if the price moves a large amount.
This is indeed what caused a certain bank to lose its barings. Again, the bank should have used other trades to hedge this risk.
In modeling this straddle we should immediately note that it is composed of two options that are constrained by their prices, dates, direction, and instruments. Figure 7 shows a straddle modeled as a sub-type of an option. As a combination option it can have components, with the constraint on the straddle defining the precise characteristics. Other sub-types of combinations would be used for other common cases: spreads, strangles, and the like.


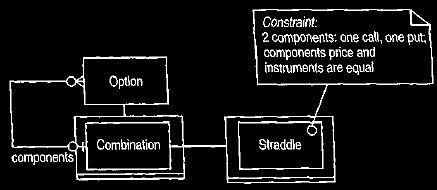
Figure 7. Modeling straddles as sub-types of options.
A straddle is a combination of a call and a put.

Use of the sub-type confirms that a straddle is a kind of option and has the same behavior as its super-type. This raises a question, however. Some behavior can be safely inherited, such as the ability to value itself and the trade date. We can think of the premium as the sum of premiums of the component options.
But what about the price? For a straddle, the components are all priced the same, so we could consider it to be the price of the straddle. Another common combination, however, is the spread. As previously mentioned, a spread is two options, but both options are the same direction (that is, two calls or two puts) at different prices. What is the price in this case? Going back to the straddle, is it a call or a put?

Figure 8 shows one way of dealing with this problem. Those attributes that can make sense at both levels can be put on an option, while the awkward attributes are placed on a conventional option. This helps to some extent but begins to fail as we recall that price was defined on the contract not the option, and that there are combinations (such as covered calls and protected puts) that combine options with regular contracts. Again, the generalization could be manipulated, but one wonders what could safely be put on the super-type.


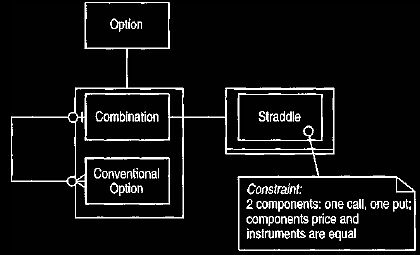
Figure 8. Separating the sub-types into combination and conventional.

These concerns are enough to raise a serious question about using composition and sub-typing together. The main problem is that, when managing risk, traders do not actually concern themselves with combinations. A combination is nothing more than the component contracts. We consider its risk the same as if the contracts were sold to separate counterparties in the same portfolio. It is the customer and the salesperson who form the combination and think of the contracts as a combination. Once the combination is dealt it behaves no differently than any other contract.

This leads us to the model shown in Figure 9. Here the salesperson's view is explicitly separated from that of the risk manager. The risk manager sees contracts, which are assembled into a product by a salesperson. The straddle is now a particular kind of product. This allows us to reconsider the behavior of the contract and move the sales-related behavior to the product while leaving the risk side of things to the contract. This includes the parties to the product who are generally irrelevant to risk management (unless exposure to a particular party is being considered). Since contracts must have a product (due to the mandatory relationship), a contract can still find its parties by collaborating with its product (but see the discussion about Clinical Observations, Section 1).


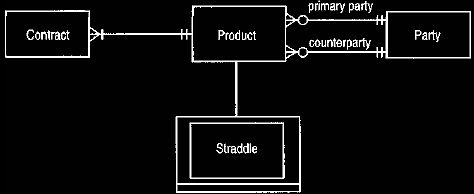
Figure 9 Introducing the product.
The product reflects the perspective of sales. In risk analysis the way in which contracts are combined as products is ignored.

In considering whether to sub-type, we need to ask two questions. The first is whether all the features of the super-type are really inherited by the sub-type. An immediate sub-typing, such as is shown in Figure 7, should be reviewed against all the features of the super-type, including features of super-types of the super-type. It is easy to forget this and be led down a dangerous path. This analysis will lead to refactoring the generalization hierarchy, and this refactoring may not be trivial. The second question we need to ask is, does the domain expert really consider the sub-typing to hold? In our example the domain expert resisted sub-typing, preferring the Figure 9 model. Later on, the Figure 8 style did reappear but has not, so far, seemed compelling enough to change the model (and the framework that implements it).

Modeling Principle: Sub-typing should be used only when all the features of the super-type are appropriate to the super-type and it makes sense conceptually to say that every instance of the sub-type is an instance of the super-type.

This leaves an interesting question as to whether it is worth putting some explicit generalization structure on the product to represent the various kinds of combinations, as shown in Figure 10. Clearly it is not for risk calculation purposes. It is useful, however, for creating new products of this form. Indeed the deepest examples of this kind of generalization are likely to lie at the application and presentation layers where specific presentations are
required for pricing and deal capture of combinations. In such situations a shared definition in the domain model is very valuable, even if the definition is currently used only in sales work. More sophisticated analysis of trades may require an understanding of how these combinations are defined.


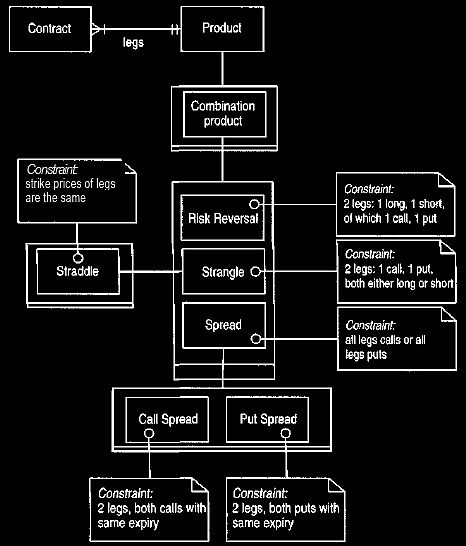
Figure 10 The common combination products.
This is a good example of a hierarchy based on constraints. The contracts linked to a product are called the legs of the product.


Example: A client has a large holding in Aroma Coffee Makers stock and is concerned about the movement in stock price over the next 6 months
before he can sell it. He might buy a straddle around the current price of $5. To the trader this product is broken down into two separate options.

Example: we wish to buy 7000 shares of Aroma Coffee Makers. The trader is not able to find a single other party who wishes to sell the exact amount.
He can find one party to sell 2000 shares and another to sell 5000 shares. we have one product with the trader to buy 7000 shares.
The product consists of two contracts for each trade.

Modeling Principle: The product/contract split should be used whenever the customer sees a single deal that is broken into several deals by the trader.

The key difference between a product and a contract is that the product represents the customer's intention while the contract refers to what actually gets traded between the counter and primary parties.

3.1 Should a Product Always Be There?
One of the consequences of the model in Figure 9 is that non-combinations are represented by a single contract and a single product.
The product is adding little to the picture (other than the separation of responsibilities between sales and risk management).

Another possibility is not to make the link to product mandatory. In such a scheme only a combination has a product. Simpler contracts have no product link. A contract has links to a party, but they are derived when a product is present. The disadvantage of this scheme is that it handles responsibilities inconsistently. A contract is responsible for handling the relationships with a party, except when it delegates the responsibilities to a product. This inconsistency can lead to a great deal of confusion. For that reason we prefer to use the model in Figure 9.

Traditional data modelers would come to the same conclusion from a different route. Normalization leads them not to wish to duplicate the links to party
and thus choose a model like Figure 9 (although it might get altered for performance reasons in a physical model). The object-oriented argument is
different because it focuses on having clear responsibilities, yet both arguments share an underlying theme: Conceptual simplicity leads us to having the minimum of base associations. In OO development this principle leads us to clearly separated responsibilities, and in relational data modeling it leads us to 14th normal form (or whatever the number is these days).

Modeling Principle: Do not duplicate base associations that have the same meanings.
Following this principle leads to types with well-separated responsibilities.

We can have as many derived associations as we like.

Modeling Principle: Be consistent in the allocation of responsibilities. Be wary of a type that sometimes is responsible for something and sometimes
delegates that responsibility. (This behavior may be correct but it should always be questioned.)

4. Sub-type State Machines

Although many common derivatives can be represented as combinations of options, this is not uniformly the case. A barrier option can either appear or disappear when the price of the instrument, as quoted on some agreed market pricing (such as a Reuters page), reaches a particular limit. Thus an option could be bought to buy (call) 10 million yen at a price of 90 JPY/USD, which would knock-in at 85 JPY/USD. This option behaves differently than a standard one. Effectively the option cannot be exercised unless the exchange rate falls below 85 JPY/USD before the expiration date. If it does fall below this barrier, then the option is knocked in and will remain exercisable whatever happens to the price between that date and the expiration. If the price never falls below the barrier level, then the purchaser can never exercise. (Barriers can also be knock-outs, in which case they can only be exercised if the exchange rate does not pass the barrier.)

This different behavior can be expressed by a modification of the state chart for a barrier, effectively replacing it with the one shown in Figure 11.
The event diagram for using it is shown in Figure 12. The only structural change is the addition of the barrier level to the option, which does work well as a sub-type of option since it provides a change in behavior and adds a new feature (the barrier level).

4.1 Ensuring Conformance of State Charts
The state chart presents an interesting issue in its own right. We can replace the state chart shown in Figure 4 with that of Figure 11, providing the
different behavior of the barrier sub-type. However, this raises a question: Are we allowed to do that? Most methods stress the importance of being able to substitute a sub-type for a super-type; this is reflected in object diagrams by only allowing us to add associations, not remove them. Many textbooks do not mention what rules govern state diagrams with sub-types. Shlaer and Mellor indicate that state diagrams can only be placed at either a super-type or a sub-type.
However, if all sub-types share a common portion, that may be placed at the super-type to ease maintainability (splicing). Rum-baugh [5] indicates that
sub-types can (usually) only add orthogonal state diagrams.



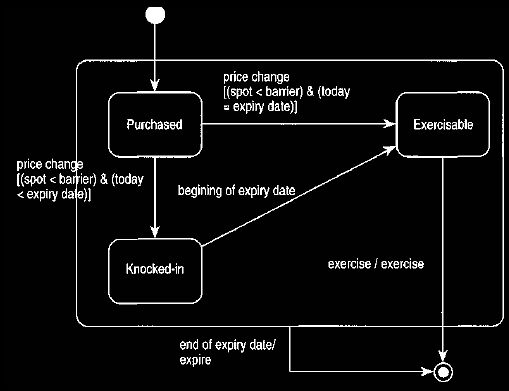
Figure 11. Harel state chart for a knock-in call.

If the instrument's price never passes the barrier, the option cannot be exercised.
After the price has passed the barrier once, it does not matter what other changes occur.


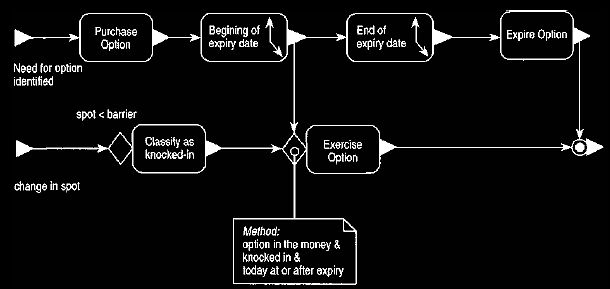
Figure 12. Event diagram of the process of using a knock-in option.

The best discussion of how sub-typing and states work is given by Cook and Daniels, who devote a whole analysis to sub-types and state diagrams. They stress the principles of design by contract which can be summarized by saying that a super-type's state chart can be extended in two ways: either by adding an orthogonal state chart or by taking a super-type's state and splitting into substates. Super-type transitions can be modified only by redirecting them to substates of their super-type's state.

Applying these guidelines to the option state models, we see a number of problems. The first lies in the treatment of the start of expiration date event. In Figure 4 (the option diagram), this causes a transition from purchased to exercisable, but in Figure 11 (the barrier diagram), the transition comes from the new knocked-in state. The end of expiration date event has a similar problem: Figure 4 shows it transitioning from the exercisable state only,
while Figure 11 has it transitioning from any state.

The first question comes from considering what an object should do if it receives an event that is not in a state in which we can do anything with it. The
object can either silently ignore the event or raise an error. Some general policy should be stated to interpret how to deal with this; for example, Cook and Daniels advise explicitly listing events in which an object is interested. Any events that normally would be silently ignored if there were no defined
transition are listed as allowable events. This resolves what would happen should the Figure 11 (barrier) diagram receive a start of expiration date event
while in the purchased start. If start of expiration date is an allowed event, it will just ignore it.

However, this is still not entirely consistent with the super-type. Figure 11 shows that when the start of expiration date event is received, a purchased
option changes to exercisable. Looking at this in contract terms, the change to purchased is part of the post-condition of start of expiration date. We cannot weaken this post-condition in the sub-type, only strengthen it. To have a knock-in call as a sub-type of an option, we must replace both state charts with those shown in Figures 13 and 14.


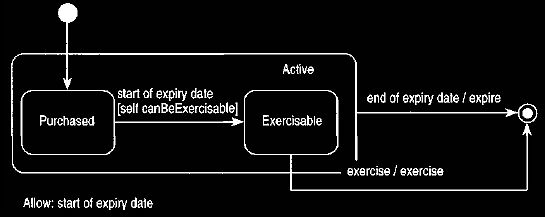
Figure 13. Modified state chart for option to allow Cook and Daniels conformance with knock-in calls.

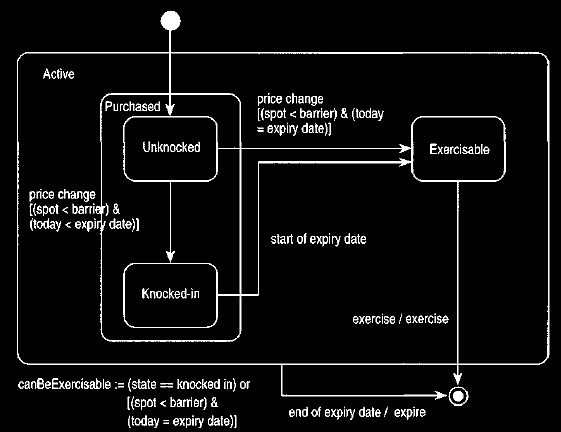
Figure 14. Modified state chart for knock-in calls to support conformance with Figure 13.

To provide conformance, these diagrams reflect two changes. The first is to generalize purchased and exercisable into an active state. We can then redirect the end of expiration date event from here. The second modification is to add canBeExercisable as a guard on the start of expiration date event. This operation is a way of saying that the start of expiration date does not always lead to the exercisable state. For regular options canBeExercisable is always true. Sub-types of an option can override it for other behavior.

Figure 14 shows how this override occurs for knock-in barriers. We introduce substates of purchased to indicate whether the barrier has been
knocked-in or not. We then split the source of the start of expiration date transition and weaken the guard to show the unguarded transition. Since we
have allowed start of expiration date on the super-type, the barrier can ignore start of expiration date when unknocked.

4.2 The Problems with Using Conformance
Having gone through this exercise of gaining conformance, we should stop and ask ourselves a few questions about the process. In our judgment Figures 4 and 11 represent simpler and clearer expressions of behavior than Figures 13 and 14. Thus, although we have gained conformance (at least
according to the Cook and Daniels definition), we have lost comprehensibility. In addition, modeling the knock-in call caused us to change the super-type diagram. It was perfectly good as it was—we only changed it because we needed a different state chart that forced us to construct a conforming sub-type state chart. This implies that a new sub-type can force us to change super-type state charts, unless we are clever enough to produce a remarkably flexible super-type state chart. Unfortunately we don't think I'm that clever, so sub-typing is going to be fraught with difficulties.
One solution to these difficulties is to recast the generalization hierarchy to avoid needing to worry about conformance. We assumed that a knocked-in call would be a sub-type of an option, each with their own state chart, as shown in Figure 15. Another approach is to treat an option as an abstract type without its own state chart and create a conventional option sub-type to hold the Figure 4 state chart, as shown in Figure 16. This avoids having to worry about the conforming state charts, allows the more natural state charts, but does introduce a separate type. It is also more consistent with the guidelines of Rumbaugh and Shlaer and Mellor, who do not discuss conformance between state models.


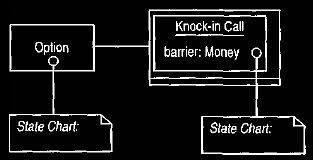
Figure 15 Knocked-in call as a sub-type of an option.
This is the natural approach, but how are the state models related?

Design by contract says that sub-types must satisfy their super-types' post-conditions. However, that does not necessarily imply that the post-condition on start of expiration date should include the transition to the exercisable state. If we choose not to include it as part of the post-condition, then the



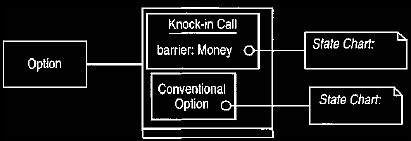
Figure 16 Creating a conventional option type.

This can make it easier to cope with the state models, but it is not as natural, original diagram is acceptable. The important thing is that start of expiration date should be allowed in all cases; whether it causes a transition or not is undefined.
This is, in fact, an example of a wider issue in using design by contract. Often people say that the post-conditions of an operation should define all
changes to the observable state of an object. This principle is often advocated by the formal methods community but is not true for design by contract. The post-condition merely specifies the state that must hold at the end of the operation. We can always indicate that nothing must change other than what is specified, but that is not assumed in the approach.
Indeed sub-typing makes such a restrictive post-condition dangerous. The whole point of sub-typing is that the super-type cannot predict all the extensions that sub-types might make. Using an overly restrictive post-condition cripples the flexibility offered by sub-typing. Post-conditions define aspects of the object's observable state that must be true. Thus any other changes can occur providing they don't violate the explicit clauses of the post-condition.

Modeling Principle: The effect of generalization on state charts is not well understood.
It is important to ensure that all events on a super-type can be handled by the sub-type. Any state chart that can be sub-typed must allow unknown events.

Modeling Principle: A post-condition defines a condition that must be true of the object after the operation. Other changes that are not mentioned
by the pos-tcondition can take place.

5. Parallel Application and Domain Hierarchies

Faced with a portfolio of various contracts, a trader might like to look at a list of the contracts together with important information about them. Such a list would show each contract on one line. The information shown on the line would vary depending on the kind of contract. The columns might be long/ short, trade date, strike price, call/put (options only), expiration date (option only), barrier level (barrier only), knock-in or knock-out (barrier only).

In this scheme some columns in the table are only relevant for certain sub-types of the option. This adds a certain amount of complexity to the problem.
What we cannot do is assume that some browser line class asks each contract for each relevant attribute. Such an approach would not work because the browser line class cannot ask a non-option for its expiration date, since by definition a non-option does not have one.

A first stage in laying out a design is to use the layered structure discussed in Analysis 12. In using this the portfolio, browser and browser line types are application facades operating as shown in Figure 17. The portfolio browser's subject is a portfolio, the browser line's subject is a contract. Neither portfolio nor contract have any visibility to the portfolio browser or browser line, since the latter types lie within the application tier and domain types have no visibility to application types (see Figure 12.6).


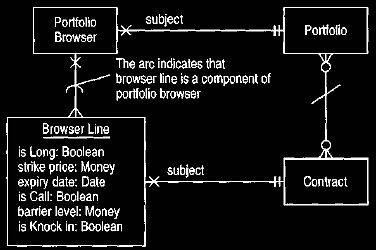
Figure 17. A portfolio browser and its relationship to the domain model.
A portfolio browser and browser line are application facades.

This structure allows a browser line to have attributes for all the columns required by the interface. As far as a presentation programmer is concerned,
each line has these attributes, which may be nil. If an attribute is nil, then that implies a blank space in the browser's table. The problem lies in the link
between the browser line and the domain model.

The browser line knows it is dealing with a collection of contracts. Unfortunately it needs to ask for information that is only defined on certain sub-types
of the contract. If a browser line asks a nonoption for its expiration date, it will get an error. Several strategies can be used to deal with this interaction: type checking in the application facade, giving the super-type an encompassing interface, using a run-time attribute, making the application facade visible to the domain model, and using exception handling.

5.1 Type Checking in the Application Facade
In this strategy the browser line is responsible for dealing with the problem. Before each request to the contract, a type check is made on the contract to ensure that the request can be issued safely, as shown in Figure 18. In C++ this takes the form of a type check, followed by a downcast, followed by the request.


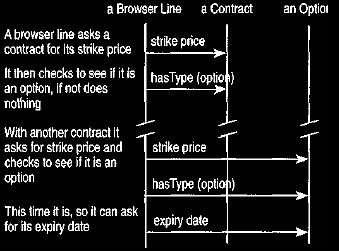
Figure 18. Interactions for type checking in the browser line.
The type is checked before an operation is called that is only defined on the sub-type.

This strategy has a number of disadvantages. The browser class, in the face of many sub-types of the contract, becomes quite complex. Furthermore any changes in the contract hierarchy causes changes in the browser. Of course, if the change is a new sub-type that introduces a new column to the browser, then such a change would be required in any case, driven by a presentation change.

The degree of type checking that this scheme implies can be reduced by a couple of approaches. We can use a subclass of browser line for each sub-type of contract.
We can use a type check to instantiate the correct subclass of browser line to do the job. Another approach is to use the Visitor pattern. Although these approaches are preferable if the degree of type checking is excessive, they still require the browser line (and its subclasses) to know about the contract hierarchy.

5.2 Giving the Super-type an Encompassing Interface
The essential problem is that it is an error to ask a contract for its expiration date. One solution is to add all of the sub-type operations to contract. Contract would naturally reply with a nil for all of these, but the relevant sub-types could override that operation to provide their value.

This approach has many problems. It becomes impossible to tell what is a truly legal operation on a contract and what is really an error. Compile-time type checking is defeated because it cannot tell which is which. Each time a sub-type is introduced, contract's interface must be altered. Thus I'm not a fan of this approach.

5.3 Using a Run-Time Attribute
Run-time attributes provide a very flexible system of adding attributes to types without changing the conceptual model. When implemented they allow attribute changes without recompilation during the execution of the system.

The basic model for contracts is shown in Figure 19, or preferably Figure 20, which uses a keyed mapping. All contracts have a number of terms, and each receives a term type. In this example each attribute of the contract and its sub-types (strike price, is call, barrier level, and so on) would be term types. If a contract is asked for a term, it replies with the value object if there is a term. In this way it is not an error to ask for a non-option's expiration date.


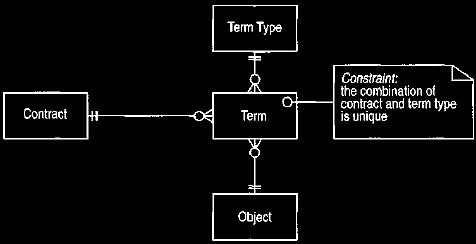
Figure 19. A run time attribute for contract.
This way asking a non-option for a property only defined on option would not cause an error.


Figure 20. Figure 19 using a keyed mapping.

Of course, this model allows a non-option to be given an expiration date by accident. This can be prevented in a couple of ways. The first is to use a
knowledge level (see Section 2.5), as shown in Figure 21. The other is to treat the term type as a derived interface. Both the model attributes (those on
contract and its sub-types) and the term type interface are provided. Updates are only provided through the model attributes.


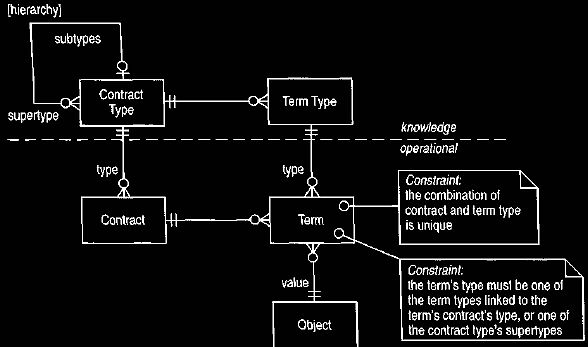
Figure 21. Using a knowledge level to control the placing of terms on contracts.
This would stop terms from being placed incorrectly on contracts but can only be checked at run-time.

Using run-time attributes does provide flexibility but it comes with significant disadvantages. First, using term types makes the interface of a contract and its sub-types harder to understand. As well as looking at the operations defined on the type, the user of a contract must also look at the instances of the term type, and indeed which instances are valid. Second, attribute types cannot be type checked at compile time, removing a very important advantage of compile-time checking. This does not matter for the browser line, since the whole point is to relax any compile-time checking, but it does matter a great deal for other parts of the system. A third disadvantage is that the basic language mechanisms are being subverted. The compiler is not aware of what is going on, and language features, such as polymorphism, must be hand-coded by the programmer. Also, run-time attributes do not perform as well as model attributes.

Many of these disadvantages can be mitigated by providing both interfaces. Those parts of the software that know about attributes at compile time can use the model attributes, and the browser can use the run-time attributes.

5.4 Making the Application Facade Visible to the Domain Model
In this approach the responsibility for loading a browser line is given to the contract that browser line is summarizing, as shown in Figure 22. Since
control is now in the contract, or its sub-type, it can load the browser line with the correct values for that sub-type. The browser line supports all necessary information for the application, and the contract or sub-type knows what is applicable for that sub-type.


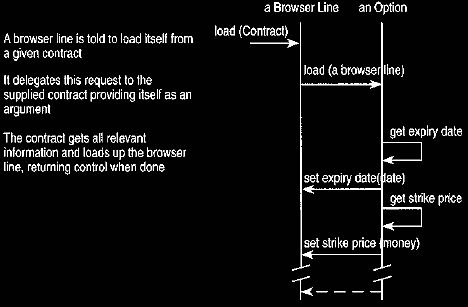
Figure 22. Interactions for contracts loading browser lines.
The browser line must be visible to the contract, which violates the usual visibility rules between domain and application tiers.

The advantages of this approach include the fact that the interaction is much simpler because no type checking is required, and a more complex interface is not needed for the contract. In addition, adding a new contract does not require the browser line to change, unless there is a corresponding change in the presentation. All that is needed is a new overriding operation to load the browser line.

The biggest disadvantage lies in the breaking of the visibility rules between application and domain tiers that are discussed in Analysis 12. This can be
avoided by placing the browser line in its own package, as shown in Figure 23. In this way the dependency from the domain model is limited to only the browser line type. Visibilities may be further reduced by splitting the browser line type into two. The presentation for the browser and the contracts use very different interfaces to the browser line. The browser line can be given its own browser line facade in the browser facade package. This facade has a simple interaction with the browser line. In this case the visibility from the browser presentation to the browser line package can be removed.


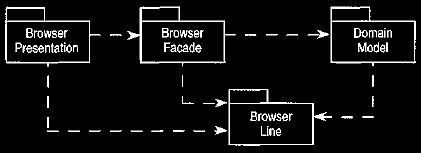
Figure 23. Visibilities for a browser line package (based on Figure 12.6).
The browser line package is a special case between the application and domain tiers.

Another disadvantage arises from the possibility of several browser applications that may have slightly different needs.
Each application would need its own browser line, which would all need to be known by contract. The splitting of browser line can help here.
One browser line facade would be created for each application, all of which would use the single browser line package.
Adding new kinds of browsers thus would not alter the contract's responsibilities unless a new feature were added to the browser line.

The fact remains that any new feature required of the browser line requires modification of the entire contract and all its sub-types. This is the fundamental trade-off between putting control in the browser line as opposed to putting control in the contract. If new contracts are added more frequently than features are added to the browser line, then we should put control in the contract. However, the change to the normal pattern of visibility is not to be taken lightly. Unless new contract sub-types occur significantly more often than changes in the browser line, we would not put control in the contract because many new sub-types in the contract would themselves imply new features to the browser line.

5.5 Using Exception Handling
Of course all of the above ideas are based on the idea that it is a bad thing to ask a non-barrier for its barrier level. With the right environment, however, this is not such a problem. If making a request of an object results in a run-time error and that error is made manifest through an exception, then the browser line can simply catch the exception and treat it as a nil. The browser line should check that the exception is actually a result of the receiver not understanding the request and not some other, more worrying error. It also assumes that it is possible to send a message to an object for which the receiver does not have an interface.
This is where a lack of type safety becomes an advantage, coupled with the exception handling features now present in the newer implementations. Smalltalk can always be used in this way, since it is untyped. Type safety can be bypassed in C++ by using a downcast.