Analysis of Exchange Trading Business

This analysis is based on a project to develop a foreign exchange derivatives trading system for a major bank.

This analysis looks at the buying and selling of goods and at the value of these goods with respect to changing market conditions. Using the experience of building a trading system for a bank, the analysis looks at buying and selling from both angles, where the bank buys and sells the same goods. The bank has to understand the value of the net effect of these trades in different circumstances.

Each trade is described by a Contract (Section 1). The contract can either buy or sell goods and is useful for businesses that need to track both directions of deals.
We can look at the net effect of a number of contracts by using a Portfolio (Section 2). We design portfolios so we can assemble them easily to select con tracts in different ways. We give the portfolio a separate object, the portfolio filter, to define the selection criteria. The portfolio filter defines an interface that can be implemented by various sub-types. This construction provides flexibility for simple and complex selection criteria. It is a useful technique for defining collections in a flexible manner.

To understand the value of a contract, we need to understand the price of the goods being traded. Goods are often priced differently depending on whether they are bought or sold. This two-way pricing behavior can be captured by a Quote (Section 3).

In volatile markets, prices can change rapidly. Traders need to value goods against a range of possible changes. The Scenario (Section 4) puts together a combination of conditions that can act as a single state of the market for valuation. Scenarios can be complex, and we need a way to define their construction so we can use the same scenario construction at different times in a consistent manner. Scenarios are useful for any domain with complex price changes.

1. Contract

The simplest kind of financial deal is that of buying some instrument from another party. The instrument can be stock, a commodity, foreign exchange, or any other commonly traded item. A basic starting point is the model shown in Figure 1. This model has a contract that is a deal with another party, referred to as the counterparty, involving some amount of an instrument. Only a single instrument is shown, although strictly speaking all trading involves two instruments - one instrument being traded for another. For most markets one instrument is always the currency prevailing in the market. The price is thus represented as a money object. Money is a sub-type of quantity (see Clinical Observations) whose unit is a currency.

In foreign exchange markets the instrument is the exchange rate. This might seem odd, but really all instruments are exchange rates. A contract to sell stock on the Dow is really a contract to exchange stock for dollars. In most cases it is easier to represent this by saying that the instrument is exchanged for the currency of the price, but for exchange rates it is better to have both currencies on the instrument and let the price be a simple number.


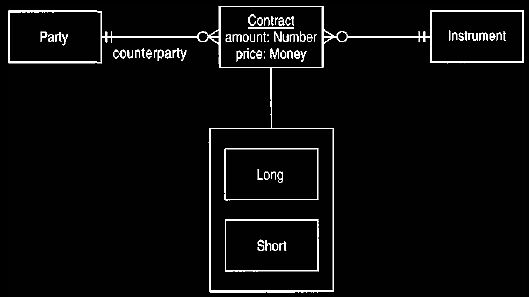
Figure 1 Simple model for a contract.
The amount of the instrument is traded with the counterparty. Long and short are terms for buy and sell, respectively.
The single counterparty limits the contracts that can be represented.

The terms long and short are the terms traders use for buy and sell, respectively. (Computer people are not the only ones with strange jargon!).
Figure 1 shows the difference between long and short with sub-typing notation. An alternative is to have a Boolean attribute isLong. Either method is acceptable, but we prefer the explicitness of Figure 1 in conceptual modeling. Sub-typing and a Boolean attribute are equivalent in conceptual modeling; sub-typing does not imply subclassing. In an implementation modeling technique (when sub-typing does imply subclassing), Figure 1 is not appropriate unless the behavior of the long and short differ (and possibly not even then). An interface model can go either way. This transformation can be made to preserve the same interface whether subclasses or flags are used.

Example: Megabank sells 1000 shares of Aroma Coffee Makers stock to Martin Fowler at $30.
This is a short contract whose counterparty is Martin Fowler, the instrument is Aroma Coffee Makers stock, the amount is 1000, and the price is $30.

Example: Megabank sells 2 million US dollars (USD) for 1 million British pounds (GBP) from British Railways.
This is a long contract in which the counterparty is British Railways, the amount is 1 million, the price is 2, and the instrument is GBP/USD. Alternatively it could be a short contract in which the amount is 2 million, the price is 0.5, and the instrument is USD/GBP.

Example: Northeast Steel sells 10,000 tons of steel to Chrysler. For Chrysler this is a long contract with a counterparty of Northeast Steel.
The instrument is steel, in which case the amount changes to a quantity to allow 10,000 tons to be represented.
(An alternative is to allow the instrument to be tons of steel, but that is less flexible for other quantities.)

This style of model is good for capturing deals done between the host organization and other parties. Often, however, deals are done internally within the host organization, such as between the options desk and the commodities desk. These internal deals are used in the management of risk. A common example is a deal to offset the risk of an option (called a hedge). Such internal deals raise the question of who is the internal party. The model shown in Figure 2 presents a more flexible way of answering this question. Two parties are shown on a contract: the long (buyer) and the short (seller).


Figure 2 Indicating buyers and sellers by separate relationships.
Having two parties supports internal deals, completely external deals, and dealing with different parties within the host organization.

In this kind of representation, the options desk and the commodities desk are represented as separate parties. If the options desk does an option with an external party and hedges it with a deal with the commodities desk, then the options desk would be a party to each contract. If the options desk were the long party in the option, it would be short in the hedge contract.

Figure 3 represents a similar situation in a slightly different way. Again the use of two relationships allows internal deals to be represented. However, here there is a notion of primary party and counterparty rather than long and short. The host bank party is always the primary party when doing a deal with an outside organization. In internal deals the choice between primary party and counterparty is arbitrary, although by convention the primary party is usually the one that initiates the deal. The sub-type of long and short is the nature of the deal as seen by the primary party.


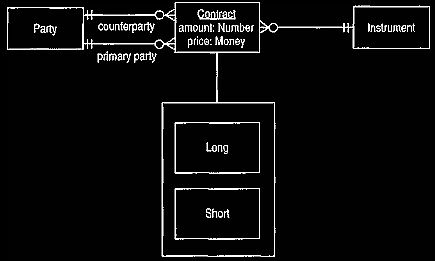
Figure 3 Counterparty and primary party.
This is less concise than Figure 2 but can better support the traders' view.

On initial analysis the model shown in Figure 3 looks less valuable than the model shown in Figure 2 because it adds an extra pair of sub-types without any great advantage. Certainly a data modeling view would reject this on the basis of a more complex data structure. The important issue, in terms of OO modeling, is interface. Is it more useful to provide operations that ask for primary and counterparty and the contract as long or short, or is it more useful to have a long and short party? It may be that the model shown in Figure 4, which essentially provides both interfaces, is the best. The deciding factor is what is most useful to the users of the concepts. For our example system, the Figure 3 model was more meaningful to the traders than that of Figure 2 and proved more useful in constructing software, although the Figure 4 interface was ultimately provided.



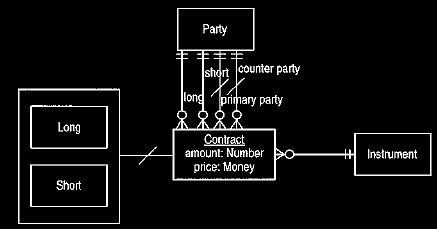
Figure 4 Using four party mappings.
This covers all points of view by deriving the duplicate elements.

Modeling Principle: When more than one equivalent set of features can be provided, pick the one that the domain expert is most comfortable with. If the domain expert feels that both are very valuable, show both and mark one derived.

The choice of what to make derived in Figure 4 is quite arbitrary. We could equally well make the long or short mapping derived. The model should not constrain the implementor who can use either kind of implementation. It could be argued that you could make nothing derived but simply use rules (such as, if the contract is short, then the short party is the same object as the primary party). We prefer to show some derivations to make the interrelationships explicit, but ultimately it is more a matter of modeling taste.

Modeling Principle: Marking a feature as derived is a constraint on the interface and does not affect the underlying data structures.

A consequence of the models shown in Figures 2-4 is that contracts can be recorded that do not involve the host bank. We can avoid this by forcing at least the primary party to be a party of the host bank. Alternatively we can ask the domain expert if holding these deals would be useful. Salespeople often like to record deals that their customers have made with other banks because it gives them information on their customers' possible risk profiles and allows them to sell a contract to improve matters. Here the flexibility of the model supports new business capabilities.

An open issue is the relationship between a contract in this trading model and a transaction in one of the accounting models from Analysis of Inventory And Accounting.
A trade can be seen as a transaction that, for example, withdraws 1000 shares of Aroma Coffee Makers stock from a Megabank account and deposits them in a buyer's account, while transferring the appropriate amount of money in the opposite direction. Both trades and transactions are useful, but for different purposes. More modeling needs to be done to explore their interrelationships.

2. Portfolio

We rarely consider contracts alone, especially when we are managing risk. Typically a bank will look at a group of related contracts and assess their joint risk. This might be the contracts dealt by a single trader, the contracts in a particular instrument, the contracts with a particular counterparty, or some other combination.

In essence a portfolio is a collection of contracts, as shown in Figure 5. Portfolios and contracts can be valued by pricing them according to some scenario. A scenario is a representation of the state of the market, either real or hypothetical (we will discuss scenarios in more detail in Section 4). The value of a portfolio is essentially the sum of the values of the underlying contracts.



Figure 5 Introducing portfolios.
A portfolio is a collection of contracts that can be valued as a whole.

A key question lies in the cardinality of the mapping from contract to portfolio. Whether a contract can sensibly lie in more than one portfolio depends on how we create and use the portfolios. If a portfolio is a trader's book, then a contract lies in the portfolio of the trader who is managing the deal. This, however, does not allow all trades with a particular counterparty to be considered together. Thus there seems to be an advantage in allowing a contract to lie in many portfolios. Portfolios can thus be built to manage risk according to different perspectives.

Using portfolios in this way raises another question, however. Suppose we need to form a portfolio that contains all contracts done with a particular counterparty. We could build an application that would search all contracts and assign them to portfolios. A better way, however, is to get the portfolio to assign contracts. We can give a portfolio a Boolean method, which takes a contract as an argument as shown in Figure 6. The portfolio then consists of all contracts for which the Boolean method evaluates to true. This allows us to construct portfolios that can select any combination of properties of a contract and then carry out the management functions of a portfolio on this derived set.


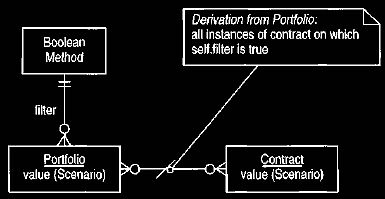
Figure 6 Dynamic portfolios with filters.
This allows portfolios to be described implicitly by properties of the contract.

Modeling Principle: If a set of objects can be formed with various criteria, a portfolio should be used.

Allowing portfolios to have methods so that they can form themselves with contracts is a powerful notion. It means that there is no need to choose a single structure to consider groups of contracts. Various structures can be used, in an ad hoc manner. Once such a structure is defined, it can be remembered as used in the future and its contents regularly updated. The structure can be defined at any time, long after the original contract was put together. In effect we are making a query, and the resulting collection of objects becomes an object in its own right.

How is the Boolean method implemented? In general the method can be any block of code that returns true or false when given a contract as an argument. Smalltalk programmers can see that assigning a single argument block as an instance variable of portfolio would provide the desired capability. C++ programmers can use roughly the same principle, although it is more tricky since C++ needs a compiled function.
This is the same problem as the individual instance methods discussed in Analysis of Inventory And Accounting, Section 6.

In the abstract the Boolean method might be the best approach, but in practice a simpler method does as well. Portfolios are commonly formed from a number of properties of contracts, including counterparty, dealer (the primary party), instrument, and dates of the deal. We can combine these attributes into a particular contract selector object, as shown in Figure 7. A contract selector is not as general as a Boolean method and can only handle a limited range of filtering. However, it is easy to set up; the user can configure it easily with a suitable user interface. If we use a contract selector to handle most of the portfolios needed by the user, we can considerably reduce the amount of programming required.


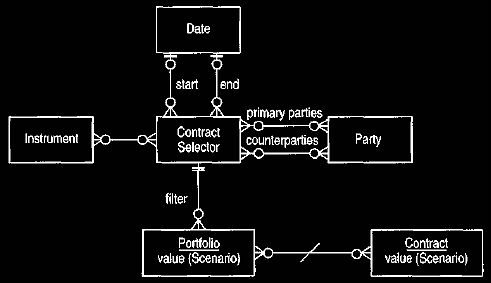
Figure 7 Contract selectors.
Note that this is an example of a parameterized method (see Section 6,6.4). It cannot select all possible portfolios,
but it can cover most portfolios used in practice more easily than the completely general case.

Example: A portfolio consists of all deals involving Aroma Coffee Makers stock sold to John Smith.
This portfolio has a filter with Aroma Coffee Makers stock as an instrument and John Smith as a counterparty.

We are not forced to choose between contract selectors and Boolean methods for our filters. We can have the best of both worlds by using the model shown in Figure 8. This model abstracts the interfaces of both the Boolean method and the contract selector into a single, abstract type—the portfolio filter. This allows us to use the contract selector for simple cases and use a range of hard-coded fiiters for more complex situations. We can easily add other portfolio filters. This is an example of the strategy pattern.

Modeling Principle: When making a process a feature of a type, the process should be given an abstract interface so that the implementation can easily vary by subclassing. A purely hard-coded implementation is one subclass, various parameter driven approaches are others.


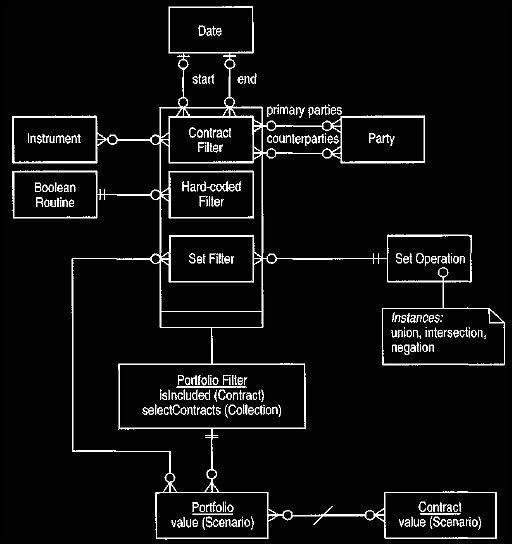
Figure 8 Provision of several portfolio filters.
This model provides both flexibility to handle the complicated cases and simple parameterization for the simple cases.
It is a combination of strategy and parameterized implementations in Analysis of Inventory And Accounting, Section 6.

The select operation on the portfolio filter takes a collection of contracts and returns another collection of contracts. For each contract in the input collection, the select operation evaluates is included and, if true, adds it to the result. Subclasses of the portfolio filter override is included to provide their specific behaviors. A portfolio may use is included to check individual contracts.

We should add a word about the naming of portfolio filter and contract selector.
Some people find the distinction between the terms quite valuable in practice. A selector selects objects of the type it is named after; thus a contract selector is used to select contracts, and it returns a collection of contracts. A filter selects some other type on behalf of its named type and is designed to be used with its named type. Hence a portfolio filter selects contracts for a portfolio. By sticking to a consistent naming, it is easier to remember the responsibilities of these two kinds of objects: The filter is only a selection mechanism, but the portfolio adds additional behavior, such as producing an overall value. In addition, the portfolio is referred to by other parts of the system, while the filter is only used for selection purposes.

Portfolios can be transient or persistent. Transient portfolios are filled on demand. The filter is specified, and all instances of the contract are checked to see if they match the filter. Once a client has finished with the portfolio, it is discarded. Persistent portfolios are created in the same way but are not discarded. When new contracts are created, they are checked against existing persistent portfolios. If they match the filter, they are added to the portfolio. Any processing based on the portfolio must then be updated, ideally incrementally. Persistent portfolios provide much faster query performance but slow down creation of contracts and use up storage. An essential modeling principle is that users should be unaware of whether portfolios are transient or persistent. Portfolios should switch from one to the other without requiring any action by the user. This requires that a new portfolio filter be checked against any existing persistent portfolio filters. If a matching one exists, then the existing portfolio should be referenced rather than a new portfolio created.

Portfolios are useful in many domains. The essential characteristic of a portfolio is that of an object that encapsulates a selection mechanism for choosing a group of objects of some type. The portfolio acts as a basis for some further summary processing. This processing can be a client object, as in this analysis, or it can be built into the portfolio itself.

Example: A car manufacturer can develop portfolios of produced cars for summarizing production and fault data. Filters can select cars according to their plant, model, shift of production, or some date range.

Example: Public health is a significant branch of health care that deals with the health of populations of patients.
We can select populations according to a range of characteristics: age, where they live, observation concepts that apply, and so on. These populations can be defined by filters, and then observations can then be made about them, such as the average peak flow rate for people who smoke more than 20 cigarettes a day. (The population is a portfolio of people where the filter is 'smokes more than 20 cigarettes a day'.)

3. Quote

Anything traded on a financial market has a price. That price, however, is not usually a single number. Two numbers are quoted: the price to buy (the bid) and the price to sell (the offer). We can model this using a pair of numbers to represent the prices, as shown in Figure 9.


Figure 9 Representing the price through two numeric properties.
An instrument can be valued using numbers or money objects. Typically stocks are valued using money but exchange rates have numbers. A quote behaves the same in either case. (We can think of a quote as a parameterized type.)

Although two numbers are common, they are not always used. Sometimes the quote is a single price, which represents the mid-value of the price. A single price is quoted with a spread—the difference between the bid and the offer. On other occasions we may see only a bid, or only an offer. This affects the way the quote is displayed. In foreign exchange markets an exchange rate such as USD/GBP might be quoted as 0.6712/5, which indicates a bid of 0.6712 and an offer of 0.6715. If only a bid is present, the quote is shown as 0.6712/; an offer-only quote appears as /0.6715.

Any object that may have two-way pricing—such as exchange rates, commodities, and so on—requires a number of behaviors as shown in Figure 10. Pulling these behaviors out into a separate quote object, as shown in Figure 11, provides all behaviors needed for two-way pricing. Anything that has a quote as a price requires a quote property.


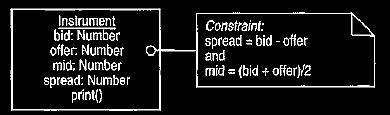
Figure 10 Behaviors required to support two-way prices.
A quote becomes a fundamental type and as such can best be represented as an attribute in those modeling methods that distinguish between attributes and object types. It is important to remember that an attribute does not represent the data structure, merely the presence of suitable operations.


Figure 11 Using a separate quote object.
This is a good approach since it brings the particular responsibilities together into a simple reusable concept.

Example: The USD/GBP rate is 0.6712/6. The instrument is USD/GBP. This instrument has a quote with a bid of 0.6712,
an offer of 0.6716, a mid of 0.6714, and a spread of 0.0004.

Example: A CD exchange sells used full-price CDs for $12 and buys them for $8. The bid is $12, the offer is $8, the mid is $10, and the spread is $4. The instrument is a full-price classical CD (even for a Chopin nocturne).

Modeling Principle: When multiple attributes interact with a behavior that might be used in several types, the attributes should be combined into a new fundamental type.

Two-way prices are common, but sometimes one-way prices are used. Modeling one-way prices is somewhat tricky. One alternative is to allow the price either to be a quote or a number. This is nearly impossible in strongly typed languages such as C++. Even in Smalltalk the client of stock is forced to determine what kind of object the price returns before doing anything with it.

An alternative is to make the quote a sub-type of the number. This can work because quotes can respond to arithmetic operations, but it still forces the client to be conscious of the differences whenever manipulating stock prices, other than for printing. In C++, where number is not a built-in type but real and integer are, this method should not be used unless a number class is provided.

Another alternative is to make number a sub-type of quote. Conceptually this has a definite appeal. Numbers are just simple quotes, and it is not too difficult to consider that every instance of a number is an instance of a quote, with identical bid and offer. (A similar argument can be used to say that number is a sub-type of complex number.) Although the argument has conceptual merit, it falls down with an interface model. For a number to be a sub-type of a quote, it must inherit the complete interface of the quote. A quote is only useful for a few domains, while a number is useful in almost every domain. Sub-typing from a quote means that the quote is used in all domains, including many where the quote's behavior is not useful. A quote must be designed so it has visibility to number, and not the other way round.

Modeling Principle: A generalization should not be used where the super-type is in a narrow domain and the sub-type is widely used.

At this point we should consider what commonalities exist between quotes in their two-way and one-way forms. Two alternatives exist: Either a one-way quote is treated as a quote, with the bid equal to the offer, or it is an error to ask for a bid or offer on a one-way quote. The former points to the presence of an abstract quote, as shown in Figure 12, while the latter avoids any such generalization. In the first alternative the client can treat the one-way and two-way quotes with the same behavior and not be concerned with differences. However, this can lead to inaccuracies because the client cannot be sure of dealing with the bid of a two-way quote. A type test operation (i sTwoWay or hasType ('TwoWayQuote')) is needed so that the client can make the test. With no abstract quote, these inaccuracies cannot occur, but the client must use the type test every time an operation is invoked to know whether the operation is safe to use.


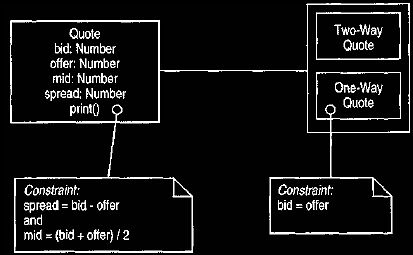
Figure 12 Abstract quote with sub-types.
One-way prices are treated as a special case of two-way prices.

The decision hinges on how often it is acceptable to ignore the difference between two- and one-way quotes. If it is almost never acceptable, then it is best not to have an abstract quote type. However, if it is frequently acceptable (which practice suggests it is), then we would strongly encourage the use of an abstract quote type. It is important to note that using the abstract quote never requires more effort by the client than not using one. It saves effort when the distinction is not required.

Modeling Principle: If the difference between two similar types is often ignored, then an abstract super-type can be used. If the distinction between them is usually important, then an abstract super-type should not be used.

Modeling Principle: If an abstract type never needs more effort for a client to use it, then it should be provided.


The abstract quote subsumes all the behavior of the sub-types because there is no additional operation or association on the sub-types. Typically we do not use subclasses to implement the sub-typing of an abstract quote, especially since such a fundamental object usually uses containment in C++. An internal flag in a quote class is a more likely implementation, especially since we often need to par a two-way quote (that is, turn it into a one-way quote) and vice versa, which requires dynamic classification.

An implicit quote can be either a buy or a sell, in which case two-way prices are not needed. Only when both buying and selling are required are two-way quotes needed.

Sometimes we want to represent the price of a contract as a quote. Often when counterparties ask the price for a contract, they do not specify the direction; in that case the trader replies with a quote. By holding on to the quote, the trader remembers what the spread was when the contract was quoted. The actual amount charged can easily be derived from the direction of the contract and the quote.


4. Scenario

The price of an instrument is never constant; otherwise, the stock markets of the world would be much less interesting places. We need to be able to show how prices can change over time and to keep a history of those changes. We can do this by placing a timepoint on the quote, as shown in Figure 13, or by placing a timepoint on the relationship between the instrument and the quote, as shown in Figure 14. The difference between the two methods is small but significant. In the former, the quote is responsible for both its two -way nature and its time-dependent behavior. In the latter method those responsibilities are separated. Since we see a quote as a fundamental type that should kept as simple as possible, we prefer to use the approach shown in Figure 14.


Figure 13 Adding a timepoint to a quote.
The timepoint indicates at what time the quote is correct for the instrument.


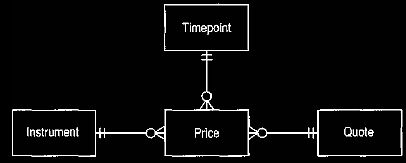
Figure 14 A price made for a stock at a particular time.
This separates the two-way behavior (quote) from the notion of a value for an instrument at a timepoint (price).

In these models, finding the closing prices for a market involves taking all the stocks within that market and looking for the latest quotes for each stock. Another alternative is to treat this collection of quotes as an object in its own right—a scenario, as shown in Figure 15.


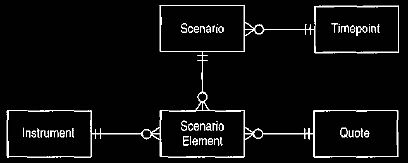
Figure 15 Scenario
This allows a group of prices at a single time to be treated as a single object.

The scenario represents the state of the market at a certain point in time, and the elements within the scenario represent the prices at that point.

If we only want to capture the published prices of a stock exchange, then a scenario seems to add little to the picture. It is easily generated by looking at the timepoints in the non-scenario model. The important question here is where the trader gets prices. One source is the exchange's public quotes. For those that manage funds of stocks, another consideration is possible future prices. Much of the effort of fund managers and traders goes into managing the risks of their portfolios as market conditions change. This risk management involves looking at alternative situations and considering their effects on prices of assets.

Example: A fund manager is managing a portfolio of stocks. She is concerned with the possibility of a fall in oil prices, which would boost the prices of many stocks but decrease the price of others, such as oil companies. This manager wants to look at several falls of differing magnitudes and consider how they affect a portfolio. Each of these falls leads to a different scenario.

Example: A production manager is assessing likely production costs for cars. The costs of raw materials and labor are instruments concerned with pricing. Several scenarios can be constructed with different likely values for these instruments.

The above examples are hypothetical cases that show the strength of the scenario approach. The scenario object provides a base to pull together all the factors in a hypothetical case so that different cases can be compared easily.

We also need to consider markets that do not have a single publisher for a price, such as the foreign exchange market. In such cases we need to add the party that is publishing the price to the model. Figures 16 and 17 show earlier models with publishing parties added. Both the scenario and non-scenario approaches are effective, and again the need for hypothetical scenarios for risk management is the deciding factor.


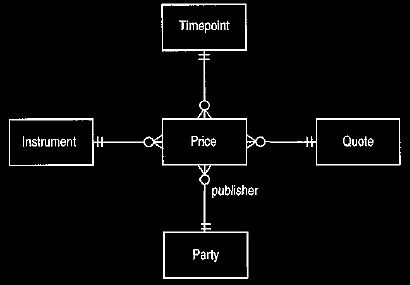
Figure 16 Model in Figure 14 with a publishing party


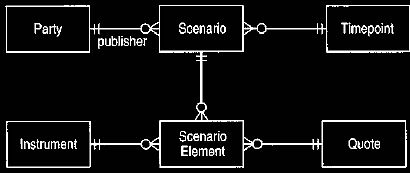
Figure 17 Model in Figure 15 with a publishing party.
Using a publisher is one more reason to use a scenario.

Example: An import/export merchant considers the prices of goods in a number of European countries. We can describe these prices by forming a scenario where the instruments are the goods he is interested in trading. By looking at the differences between these markets, using two-way prices, he can look for opportunities where the price difference is greater than the cost of transporting the goods (a process referred to as arbitrage).

Modeling Principle: Scenarios should be used when a combination of prices or rates should be considered as a group.

4.1 Defining How to Build a Scenario
Where do prices come from? In some cases this can be a simple question, for instance, when prices are published by an exchange. In other cases, particularly when there are hypothetical scenarios, more complex schemes might be used.

In broad terms we can see three origins of a price: publication by some body that is widely quoted in the market, calculation from other prices or market characteristics, or the opinion of an individual trader or team of analysts. The first case, shown in Figure 18, is the most straightforward. Instructions are required to source the relevant information. Typically these instructions come from a source, such as Reuters, that tells where to look for information (for example, "Page 3, second column of the row starting IBM").


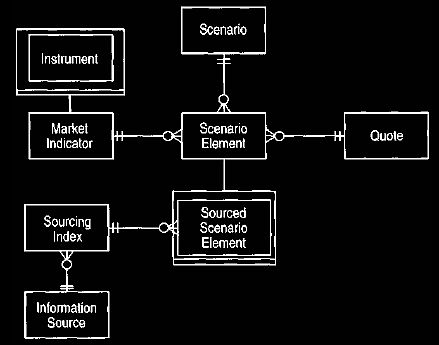
Figure 18 Sourcing a scenario element.
This model describes where a particular element comes from.

In effect, using a published price makes the quote for a sourced scenario element derived. Rather than asserting the quote for a sourced scenario element, we derive it using the sourcing index. There is thus an argument for making the link to a quote a derived link. This can be done safely if the link can never be asserted, as when a trader records a hunch. Asserting the quote can cause problems because sometimes the quote can be asserted and sometimes derived. One way out of this is to use a notation for hybrid or option ally derived relationships (see Odell [2], page 56). This seems to take the derived issue too far. We tend to notate according to the most common case and describe what happens precisely in the supporting documentation.

Example: An analyst looking at prices for mail order goods can treat each company as an information source. The sourcing index can be a page number in a catalog. There can then be a separate scenario for each retailer, or an overall scenario can be built that combines all retailers. Rather than asking for the price of an instrument, questions such as lowest price and average price of some instrument are supported.

Figure 18 introduces market indicator as a super-type of instrument. This reflects the fact that scenarios can contain things other than instruments. For derivatives, an important part of the pricing approach is the volatility of an instrument—a number that indicates how much the value of the instrument is changing. This volatility is not an instrument that can be traded, but it is recorded in a scenario in the same way as an instrument. Hence a market indicator includes volatilities, as well as all instruments.

Example: Foreign currency markets have many market indicators that are not instruments, including interest rates on the various currencies and the volatility of an exchange rate—an indication of how much the exchange rate is changing.

Example: An analyst looking at prices for mail order goods is interested in the increase in jeans prices.
Jeans price increase becomes a market indicator but not an instrument. Jeans are both a market indicator and an instrument.

Calculating scenario elements is also straightforward. The key is to accept that the algorithm for calculating the price can be an object in its own right. A simple example of this is cross-rates used in foreign exchange. If we know the exchange rates for USD/DEM and for USD/GBP, then we can calculate the exchange rate for GBP/DEM as (USD/DEM) / (USD/GBP). We can represent this by having a cross-rate scenario element, which we model by having a sub-type of scenario element that references other scenario elements for the numerator and denominator of the cross-rate, as shown in Figure 19. The quote for the cross-rate scenario element is then derived from the quotes for the denominator and numerator scenario elements.



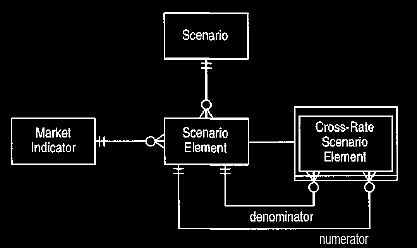
Figure 19 Calculating scenario elements by cross-rates.
This can be used to determine a third element from the ratio of two known elements.

Note that the denominator and numerator are expressed as scenario elements rather than market indicators. If we are just expressing cross-rates as numerator described above, then referencing the market indicators seems the most sensible (USD/GBP is a market indicator). However, the whole point of providing scenarios is to allow us to post several different prices, under different assumptions, for the same market indicator. Referencing the scenario element allows us to focus on which of these prices we are to use. There might be two USD/DEM figures: one from Reuters and one from LIBOR. By referencing the scenario elements, we are able to indicate which one we want.

Example: A trader is a specialist on the French franc. She determines the exchange rate between Dutch guilders (NLG) and French francs (FFR) by cross-rates using the German mark (DEM). She does this by creating a cross-rate scenario element. The market indicator for this scenario element is NLG/FFR. For the numerator she uses the NLG/ DEM rate quoted by Reuters; that is the scenario element for the instrument NLG/DEM in the Reuters scenario. However she does not get the DEM/FFR rate for the denominator from Reuters; instead she uses her own scenario (built on the basis of her own specialized knowledge). Thus she forms the cross-rate from scenario elements in different scenarios.

The kind of approach used for cross-rates can be used for a number of common calculations, where new kinds of calculations are supported by new sub-types of the scenario element. Figure 20 shows a generalization of this structure. In this case the calculated scenario element has a list of scenario elements as arguments and a formula. The formula represents the algorithm for the calculation, which uses arguments provided to it by the arguments on the calculated scenario element. For the cross-rate the formula is arg[1] / arg[2].


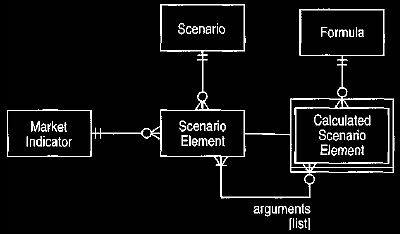
Figure 20 A more general approach to calculated scenario elements.
The formula can be a spreadsheet-style formula based on the arguments. It supports a range of arithmetic combinations of scenario element.

The actual arguments are provided by the calculated scenario element. This allows a single formula to be reused by several calculated scenario elements. The cross-rate for GBP/DEM uses the formula with arguments <USD/DEM, USD/GBP>, and the GBP/JPY cross-rate uses the arguments <USD/JPY, USD/GBP>. Note the importance of providing the arguments as a list rather than the usual set for multivalued mappings. The position is essential for the formulas to be correctly written.

Example: The price change for jeans is calculated by a calculated scenario element that takes the difference between prices of jeans in this year's scenario and last year's scenario.

We can implement the formulas in several ways. One way is to hard-code formulas in the implementation language. Since common formulas (such as cross-rates) are widely reused, hard-coding is not a disadvantage in this case. If the number of formulas is small and does not change too often, this is the best approach. Even if a new formula is added every month, this would be fairly easy to control even for a complex system. We can use a more sophisticated approach if we want to give the user the ability to add formulas. We can build an interpreter [1] that recognizes a simple range of formulaic expressions. This technique is familiar to any user who has used spreadsheets. We could provide an interactive formula builder, but any user who can build a formula can probably type a spreadsheet-like formula. The interpreter [1] thus does not have to recognize all possible formulas. It is perfectly all right to have some formulas built by the parser and some hard-coded. The software for scenario elements does not care how a formula is built but is concerned with providing arguments to the formula that generate the calculated quote. Following the best principles of object-orientation, interface is separated from implementation. (For further discussion on this Analysis of Inventory And Accounting, Section 6)

Modeling Principle: To make a process a feature of a type, the process must have an abstract interface so that the implementation can easily vary by subclassing. A purely hard-coded implementation is one subclass; various parameter driven approaches are others.

The interaction diagram shown in Figure 21 reveals some useful points about how this behavior might work. First note how the formula is given a list of quotes as input, rather than a list of scenario elements. This is mildly arbitrary, but providing the same thing as input as is returned as output is a useful policy to follow. Without this, coders can quickly get confused about the type of things they are dealing with. This, of course, assumes that the arithmetic operations are all defined with a quote, which would be a natural place to deal with two-way price arithmetic. In this case we can set up the formulas so that they work on anything that supported arithmetic, not only quotes.


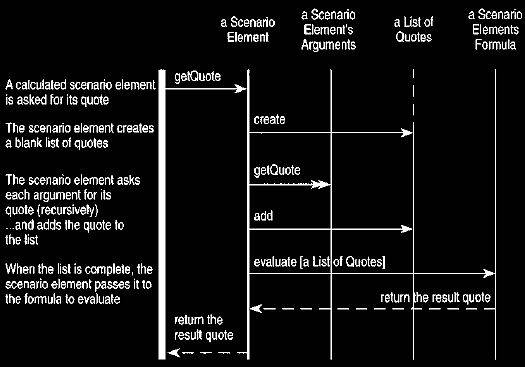
Figure 21 Interaction diagram for calculated scenario elements.
The behavior is naturally recursive in that the getQuote operation calls getQuote on all the arguments, potentially resulting in a long chain of calculations.
This, like many recursive structures, is very elegant (but difficult to show on an interaction diagram). In practice, however, it can lead to quite a
number of redundant calculations. A caching policy for calculated quote values is needed to prevent unnecessary recalculation caused by repeated calls of getQuote to the same object. As with any cache, of course, we have to ensure that the cache is properly updated when a source value changes. We can use the arguments mapping in the reverse direction to reset all dependent scenario elements.

Modeling Principle: When information can be retrieved from an information source or calculated from other available figures, an abstract interface with sourcing and calculation as subclasses should be provided.